背景
最近在抓公众号的文章,处理完一批文章特征后,已知这些特征就可以知道每个文章之间的余弦相似度(即距离),我想如何可视化的把结果展示出来,就想着把这些文章用3D的形式渲染出来,可是只知道距离没有3维坐标就没办法渲染成3D视图。
数据列表:
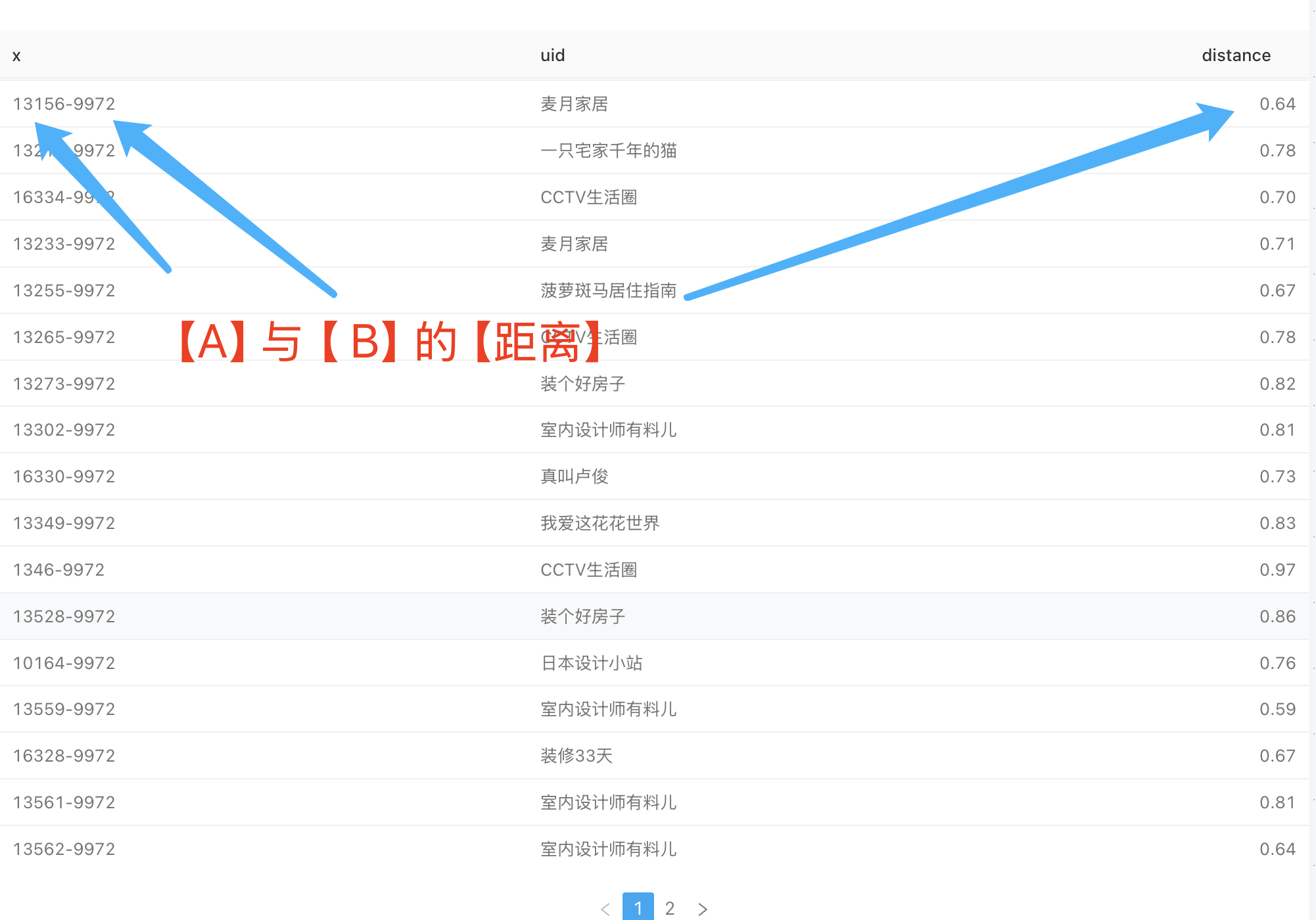
逻辑和代码实现
各点之间的距离如下:
- A -> B 距离 1
- A -> C 距离 2
- B -> D 距离 1.5
- C -> D 距离 1.8
那么可以梳理出如下表格:
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 2 | 未知 |
| B | 1 | 未知(数据漏写或懒得写) | 未知 | 1.5 |
| C | 2 | 未知 | 0 | 1.8 |
| D | 未知 | 1.5 | 1.8 | 0 |
多维尺度分析的步骤如下:
- 将部分已知的距离矩阵补全,形成完整的对称矩阵。如果仅有部分距离数据,可使用默认值(例如最大距离)来填充未知值。
- 计算距离矩阵的双中心化矩阵。
- 对双中心化后的矩阵进行 特征值分解 或 奇异值分解。
- 选择前
dimensions个最大特征值对应的特征向量生成低维坐标。
下面是numeric.js的实现方式
<!-- 引入 numeric.js 库 -->
<script src="https://lf3-cdn-tos.bytecdntp.com/cdn/expire-1-M/numeric/1.2.6/numeric.min.js"></script>
<script>
// 示例数据:已知部分距离
const knownDistances = [
[0, 1, 2, null],
[1, null, null, 1.5],
[2, null, 0, 1.8],
[null, 1.5, 1.8, 0]
];
// MDS 算法:已知部分距离生成三维坐标
function mds(knownDistances, dimensions = 3) {
const n = knownDistances.length;
// Step 1: 补全距离矩阵
const completedDistances = knownDistances.map(row =>
row.map(val => val !== null ? val : Math.max(...knownDistances.flat().filter(x => x !== null)))
);
// Step 2: 计算双中心化距离矩阵
const squaredDistances = completedDistances.map(row => row.map(d => d ** 2));
const totalMean = numeric.sum(squaredDistances.flat()) / (n * n);
const rowMeans = squaredDistances.map(row => numeric.sum(row) / n);
const colMeans = Array.from({ length: n }, (_, j) =>
numeric.sum(squaredDistances.map(row => row[j])) / n
);
const B = squaredDistances.map((row, i) =>
row.map((val, j) => -0.5 * (val - rowMeans[i] - colMeans[j] + totalMean))
);
// Step 3: 计算 B 的特征值和特征向量
const svdResult = numeric.svd(B);
const eigenValues = svdResult.S;
const eigenVectors = svdResult.U;
// Step 4: 选择前 `dimensions` 个最大特征值对应的特征向量
const topEigenValues = eigenValues.slice(0, dimensions).map(Math.sqrt);
const topEigenVectors = eigenVectors.map(row => row.slice(0, dimensions));
// Step 5: 计算降维坐标
const coordinates = topEigenVectors.map(row =>
row.map((val, j) => val * topEigenValues[j])
);
return coordinates;
}
// 生成并输出三维坐标
const coordinates = mds(knownDistances, 3);
console.log("3D Coordinates:");
console.log(coordinates);
</script>
效果:
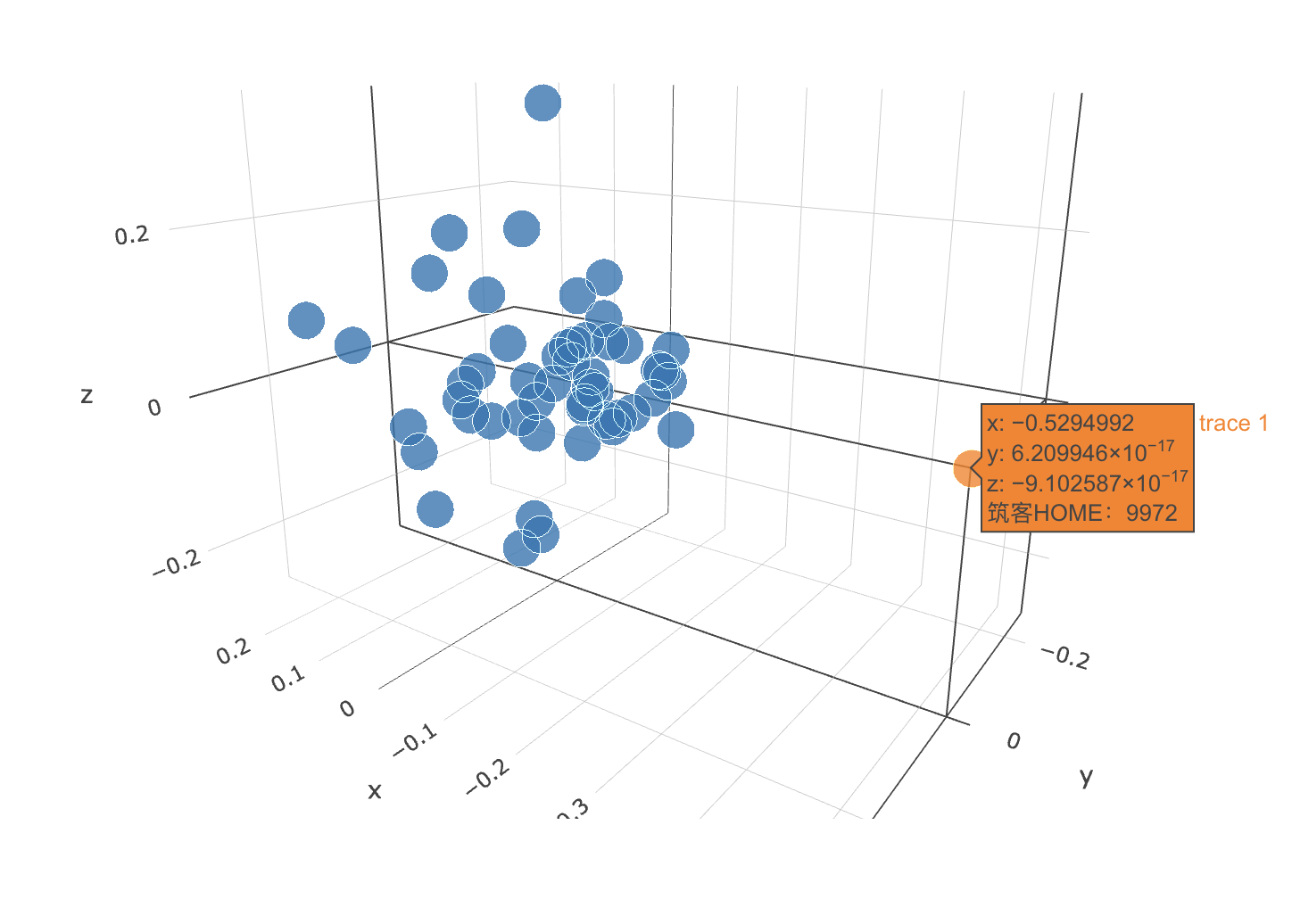
代码解析
-
补全距离矩阵:使用已知的最大距离填补矩阵中的
null值,生成对称的完整矩阵。 -
计算双中心化矩阵 B:对已补全的距离矩阵进行双中心化,即将其转换为内积矩阵 B,用于后续分解。这一步使用了 MDS 的核心公式。
-
奇异值分解:对中心化后的矩阵 B 进行 SVD 分解,得到奇异值和奇异向量。
-
选择主成分并计算降维结果:选取最大的几个奇异值对应的奇异向量,并根据奇异值的平方根得到降维坐标。
适用情况
这种方法适用于已知部分距离的情况,并通过距离矩阵补全和 MDS 降维来生成三维坐标